RL_Importance_Sampling

Importance Sampling

1.What is Importance Sampling

Importance Sampling(IS) is a general technique for estimating properties of a particular distribution $p$, while only having samples generated from a different distribution $q$ than the distribution of interest($p$).

And actually, IS is a variant of Monte Carlo approximation. In Monte Carlo approximation, we were extimating the expected value of a random variable $X$ by this sample mean sum:

$E(X) \approx \frac{1}{n}\sum\limits_{i = 1}^{n}x_i,where, X\sim p,x_i\sim p$

But, there is a big assumption that we can efficiently draw samples from the true distribution $p$ of this random variable $X$. What if we can’t do that? Can we use some alternative distribution like $q$ and use the samples drawing from $q$ to correct the fact that we were drawing samples from the wrong distribution or get a better estimation than its true distribution $p$? There is where Importance sampling comes for.

In Importance Sampling, where $p$ is the true distribution of random variable $X$, and $q$ which is called proposal distribution that we use to sampling, and $q$ satisfied absolute continuity that $\forall q(pdfs), s.t. q(x) = 0 \rightarrow p(x) = 0$:

$E_p[X] = \sum\limits_{x}xp(x) = \sum\limits_{x}x\frac{p(x)}{q(x)}q(x) = E_q[x\frac{p(x)}{q(x)}] \approx \frac{1}{n}\sum\limits_{i=1}^{n}x_i\frac{p(x_i)}{q(x_i)}, \quad where, x_i\sim q$

Finally, an unbiased estimator of the true expectation(Monte Carlo estimator is unbiased).

$E_p[X] \approx \frac{1}{n}\sum\limits_{i=1}^{n}x_iw(x_i), \quad where, x_i\sim q, w(x_i) = \frac{p(x_i)}{q(x_i)}$

$w(x)$ is called the importance weight , it will give more weight to the values that may appear more possible under its true distribution. And IS is worked no matter whether the $p$ is normalized, something like $p(x) = \frac{h(x)}{Z}$ or not.

$E_p[X] = \sum\limits_{x}xp(x) = \sum\limits_{x}x\frac{h(x)}{Z} = \sum\limits_{x}x\frac{h(x)}{q(x)Z}q(x) \approx \frac{1}{Z}\frac{1}{n}\sum\limits_{i=1}^{n}x_i^q\frac{h(x_i^q)}{q(x_i^q)}$

Now, $E_p[X=1] = 1 = \sum\limits_{x}\frac{h(x)}{Z}$, we can get:

$Z = \sum\limits_{x}h(x) = \sum\limits_{x}\frac{h(x)}{q(x)}q(x) \approx\frac{1}{n}\sum\limits_{i=1}^{n}\frac{h(x_i^q)}{q(x_i^q)} = \frac{1}{n}\sum\limits_{i=1}^{n}w(x_i^q) = \bar{w}$

So, finally,

$E_p[X] = \frac{\bar{xw}}{\bar{w}}$

2. A bad choice of $q$ makes thing worse.

Moral: Choose $q(x)$ large where $|x|p(x)$ large.

Importance sampling is a variance reduction technique that can be used in the Monte Carlo method. The idea behind importance sampling is that certain values of the input random variables in a simulation have more impact on the parameter being estimated than others. If these “important” values are emphasized by sampling more frequently, then the estimator variance can be reduced. Hence, the basic methodology in importance sampling is to choose a distribution which “encourages” the important values. This use of “biased” distributions will result in a biased estimator if it is applied directly in the simulation. However, the simulation outputs are weighted to correct for the use of the biased distribution, and this ensures that the new importance sampling estimator is unbiased. The weight is given by the likelihood ratio, that is, the Radon–Nikodym derivative of the true underlying distribution with respect to the biased simulation distribution.(From Wikipedia)

The fundamental issue in implementing importance sampling simulation is the choice of the biased distribution which encourages the important regions of the input variables. Choosing or designing a good biased distribution is the “art” of importance sampling. The rewards for a good distribution can be huge run-time savings; the penalty for a bad distribution can be longer run times than for a general Monte Carlo simulation without importance sampling.(From Wikipedia)

Now, let $I = \frac{1}{n}\sum\limits_{i=1}^{n}x_iw(x_i)$, the variance of $I$,

$\sigma^2(I) = \frac{1}{n}\sigma^2(X\frac{p(X)}{q(X)})$

a litte bit different from the standard Monte Carlo variance:

$\sigma^2(I) = \frac{1}{n}\sigma^2(X)$

So this is how you can improve the expected error you can lower the expected error of your estimator by reducing this variance, because the mean square error is $mse = bias^2 + var$. It could be worse if you made a bad choice of $q$, a high variance made it hard to learn or converge. Also it could be much samller if you choose a good $q$. Often, people try to make $q$ as close to $p$ as possible.
For example: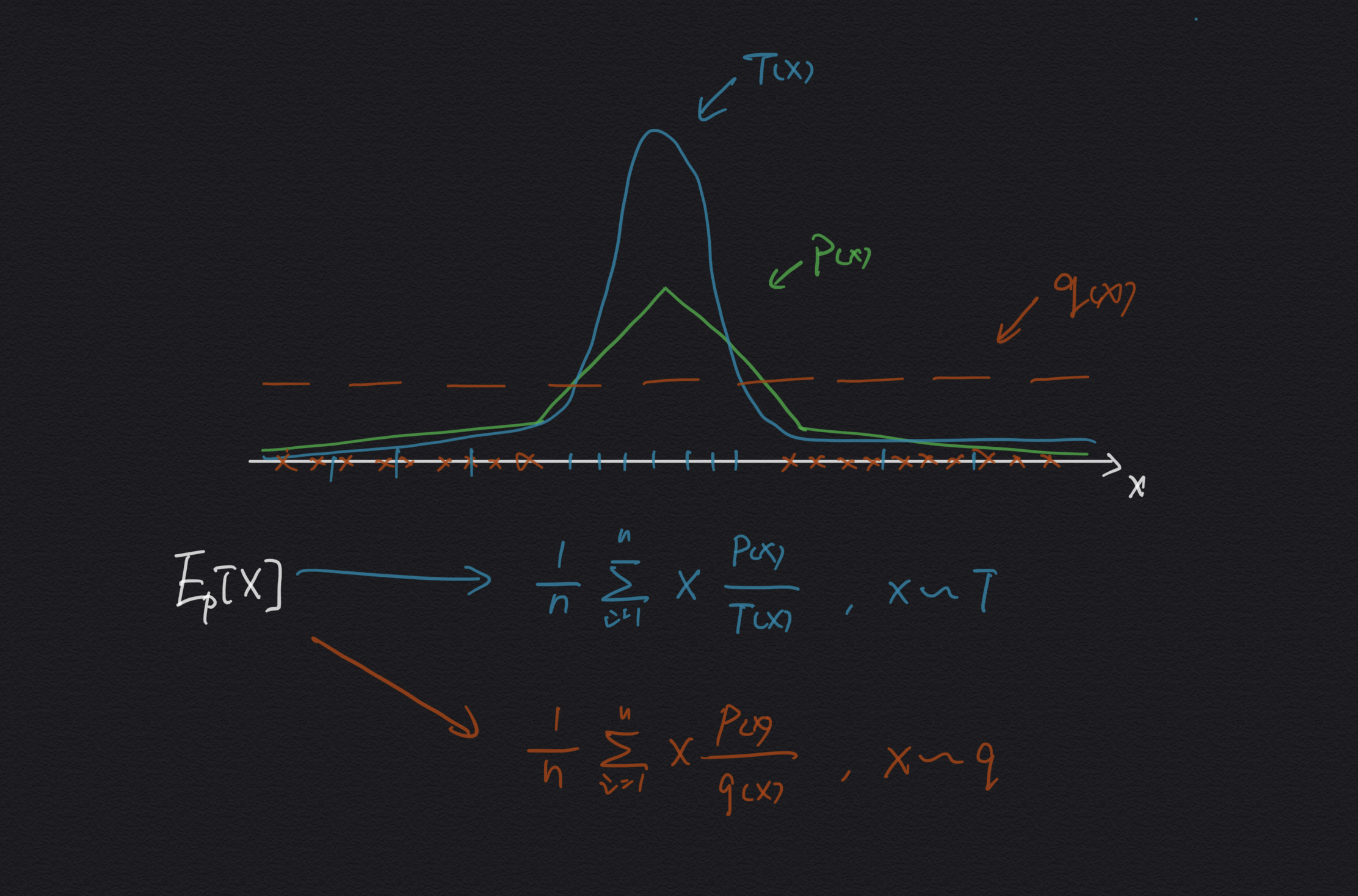

There are two proposal distributions $q$ and $T$ that we can use to estimate the expect value of $X$ which is under its true distribution $p$. If we choose to use $q$ distribution, we will get a high variance because under the $q$ distribution in most time the samples we get have a very small importance weights that don’t contribute to the estimator much, and occasionally it will get a very large importance weight when the sample appears in the middle part, and that makes it struggle to estimate from $q$ distribution. But for $T$, because in most time, we will get the samples from its middle part where have a relatively smooth importance weights that eventually get a much smaller variance than $q$, and that makes it converge much more quickly than $q$.

There is an optimal equation to choose the proposal distribution $q$:
Let $\mu = E_p[|X|] = $, if we choose a $q$ that: $q(x) = \frac{p(x)|x|}{\mu}$, we can get a zero-variance estimator.

3. Applications

Such methods are frequently used to estimate posterior densities(后验密度估计) or expectations in state(状态期望值) and/or parameter estimation problems in probabilistic models(概率模型中的参数估计问题) that are too hard to treat analytically, for example in Bayesian networks.

4. Conventional biasing methods

Sacling:
Shifting probability mass into the event region $X\geq t$ by positive scaling of the random variable $X$, with a number greater than unity has the effect of increasing the variance (mean also) of the density function. This results in a heavier tail of the density, leading to an increase in the event probability. However, while scaling shifts probability mass into the desired event region, it also pushes mass into the complementary region $X {<} t $, which is undesirable.

$f_{*}(x)={\frac {1}{a}}f{\bigg (}{\frac {x}{a}}{\bigg )}, w(x)=a{\frac {f(x)}{f(x/a)}}$

Translation:
Another simple and effective biasing technique employs translation of the density function (and hence random variable) to place much of its probability mass in the rare event region. Translation does not suffer from a dimensionality effect and has been successfully used in several applications relating to simulation of digital communication systems. It often provides better simulation gains than scaling. In biasing by translation, the simulation density is given by

$f_{*}(x)=f(x-c),\quad c>0$

where $c$ is the amount of shift and is to be chosen to minimize the variance of the importance sampling estimator.

5. Evaluation of importance sampling

In order to identify successful importance sampling techniques, it is useful to be able to quantify the run-time savings due to the use of the importance sampling approach. The performance measure commonly used is $\sigma _{MC}^{2}/\sigma _{IS}^{2}$, and this can be interpreted as the speed-up factor by which the importance sampling estimator achieves the same precision as the MC estimator.

6. Importance Sampling in Deep Reinforcement Learning

We often see this term in reinforcement learning paper, like the “Prioritized experience replay”, “PPO”,etc. And now, we’re going to explore why they use IS, and how they use it.

Prioritized Experience Replay
The importance weight here is:

$w_i={\bigg (}{\frac {1}{N}\frac {1}{P(i)} }{\bigg )}^{\beta} / max_i w_i$

There are two excellent explanation about the Importace Sampling Correction appears in PER:

TL;DR the importance sampling in PER is to correct the over-sampling with respect to the uniform distribution.

In paper Prioritized Experience Replay, it said: “In particular, we propose to more frequently replay transitions with high expected learning progress, as measured by the magnitude of their temporal-difference (TD) error. This prioritization can lead to a loss of diversity, which we alleviate with stochastic prioritization, and introduce bias, which we correct with importance sampling. “

And DeepMind describes why we need an Importace Sampling Correction:

The estimation of the expected value with stochastic updates relies on those updates corresponding to the same distribution as its expectation. Prioritized replay introduces bias because it changes this distribution in an uncontrolled fashion, and therefore changes the solution that the estimates will converge to (even if the policy and state distribution are fixed). We can correct this bias by using importance-sampling (IS) weights.

Now the loss we want to minimize in DQN is:

$L_i(\theta_i) = E_{(s, a, r, s') \sim U(D)}[(r + \lambda max_{a'}Q(s', a';\theta_i^{-}) - Q(s_i, a_i;\theta_i))^2]$

Let $X = (r + \lambda max_{a’}Q(s’, a’;\theta_i^{-}) - Q(s_i, a_i;\theta_i))^2$ which should under its “true” distribution $U(D)$ - the Uniform Distribution($1/N$), but now the samples $X$ we get are under the stochastic prioritization distribution $P$, so we need the Importance Sampling Correction to down-weight those samples with high prority which has a higher $P(i)$ to be choose to eliminate the bias it brings. Incidentally, the $\beta$ here is a kind of bias-variance trade-off method, as $\beta$ grows from $\beta_0$ to $1$, the bias is gradually eliminated, which means IS is more important near convergence.

But why we don’t use Importance sampling in DQN?
The important property here is the sampling Q-learning does is over the probability distribution of the environment state transitions, not over the policy distribution. Consequently, we don’t need to correct for different policy distributions!

REFERENCES

Wikipedia:

Importance Sampling

Videos: